An Investigation using Tidal Gauge Data Part 1 – Preliminary Analysis
by Dr. Alan Welch FBIS FRAS — 2 December 2025
Note: This paper will be published in two mutually-dependent parts, this part and the second to follow in day or two, depending on the publishing schedule here.
Introduction
The question “Why does the Global Sea Level Rise have a sinusoidal variation with a period of about 26 years?” was asked in the comments to one of my papers in 2023. My reply pointed out that the satellite coverage was only 95% and so what was happening in the other 5% may be relevant. In my follow up paper “Measuring and Analysing Sea Levels using Satellites during 2023 – Part 2” . I analysed the Tidal Gauge results of 9 ports in the northern regions of the Atlantic Ocean and above up to the Arctic Ocean. The analysis was very simplistic but showed promise so now a more detailed analysis will be carried out using procedures and methods developed more recently.
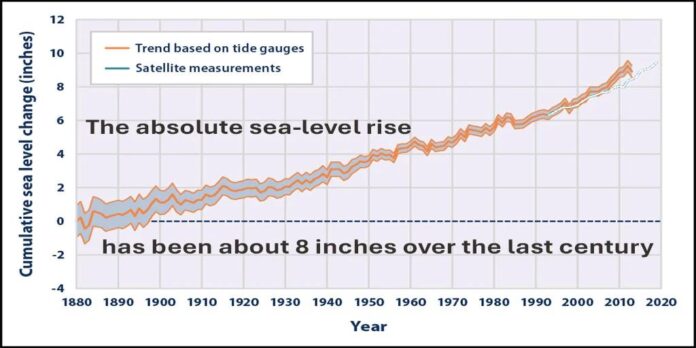
Before proceeding another question could be “so what?”. The graph is basically almost linear (R2 = 0.99) with fits using quadratic or sinusoidal adding very little on this. But in 2018 Nerem et al produced their paper concentrating on a quadratic curve, using the small quadratic coefficient to be representative of an acceleration. If they had contained this to the confines of the data all would have been acceptable, but they proceeded to extrapolate for over 80 years and release their paper. The paper as still being used as a reference in many papers each month. Over the 8 years it has been used to create dramatic scenarios of flooded cities and frighten all the children. The investigation of a sinusoidal curve has tried to balance the picture. A point overlooked in using the quadratic curve is that if the calculations had been started in 2008, they would now show a deceleration. What paper would Nerem et al then write?
The paper is in two parts.
Part 1 contains preliminary analyses in which each Tidal Gauge is processed up to the Spectral Analysis stage.
Part 2 carries out Curve Fitting in which residual values (Actual values minus values on a best fit curve) are judged against a curve that is the combination of 2 or 3 sinusoidal curves using peak periods derived from the spectral analyes.
Preliminary Analysis
This study makes more use of Tidal Gauge data than NOAA data but uses Spectral Analysis.
The 9 locations are Reykjavik – Iceland Torshavn – Faroe Islands
Aberdeen – Scotland Lerwick – Scotland Bergen – Norway Barentsberg – Svalbard Narvik – Norway Murmansk – Russia Tiksi – Russia
Only Aberdeen and Bergen have datasets spanning more than 100 years, with Torshavn covering only about 50 years.
Before analysing these 9 ports the results for Brest will be studied as this covers over 210 years although there are a couple of sizeable breaks in data. This work was carried out earlier, but some aspects will be of interest. The data are shown in Figure 1.

Figure 1
The usual curve fitting is carried out as shown in Figure 2. Again, possibly excessive precision has been used to be on the safe side. This is not in order to indicate accurate fitting but with possible high values on the “x” axis power terms might need this extra precision.

Figure 2
A Spectral Analysis was carried out on the data and Figures 3 and 4 show the outcome for long and short periods.

Figure 3

Figure 4
Figure 3 indicates a peak (barely a peak) at a period of 1429 years. Most other Tidal Gauges show much higher periods, but it would be interesting to see how sinusoidal curves with periods in the region of 1000 years would compare with the quadratic fit.
Curve fitting was carried out for curves with periods of 1000, 1100 and 1200 years. The equations are shown in Excel Format.
= CONST + AMP * SIN(((SHIFT + 2 * A1)/PERIOD) * PI()) (Equation 1)
| CONST | AMP | SHIFT | PERIOD |
| mm | mm | years | years |
| 7341.5 | 406.5 | 1409.0 | 1000 |
| 7371.2 | 437.5 | 1575.4 | 1100 |
| 7430.1 | 496.9 | 1731.4 | 1200 |
Figures 5,6 and 7 compare the quadratic curve with the 3 sinusoidal curves, together with comparisons of slope and acceleration.

Figure 5

Figure 6

Figure 7
The next part may be good lateral thinking or a bit more La La Land!!
Using the 1200 year curve and extrapolating from 500 BC to 2500 AD results in the following.

Figure 8
The indicated periods may be arguable. It surprised me that the last Thames Ice Fair occurred as late as 1814. A more worrying interpretation of this graph, if it is remotely indicative, would be that the sea levels (and associated Temperatures) do not peak until about 2450. Could events be as bad as that? How hot were the Roman and Medieval Warm Periods?
Finally with respect to Brest Figure 9 shows the residuals, that is the actual values minus the values on the quadratic curve and Figure 10 the spectral analysis of these residuals.

Figure 9

Figure 10
The periods of the peaks vary from those on the full data spectral analysis, and it is not very easily seen on figure 9 that there may be a decadal oscillation of about 93 years. This was
investigated by creating data files of random values, one set as straightforward random values and one set as random numbers with a standard variation. Many cases were run and figures 11 and 12 show one case from each series.

Figure 11

Figure 12
First impressions are a bit worrying as they indicate curves with periods in the range 10 to100 years but closer inspection shows these all have small amplitude (labelled theta on these plots) of about 2 whereas in the actual tidal gauge plots these are between 10 and 30 for the residuals. These Theta values are relative values and do not indicate actual physical values.
(I may not have described the process clearly, and may not have described it correctly, so if anyone out there can help I would be very grateful)
Turning now to the 9 Tidal Gauge datasets they will be considered starting with the longest period of measurement and then in roughly an order of reducing period. But before proceeding the following 9 small figures (in Figure 13) show the outcome of the earlier curve fitting exercise of a 26-year period curve to plots of the residual values, that is the actual values minus the value on the quadratic fit. Whilst a roughly 26-year period curve fits in many positions there is evidence of other, usually, longer period components as can be seen in the Aberdeen plot where a larger 85ish year variation is obvious. The larger spectral analysis peaks will refer to primary modes, but shorter ones may be other primary modes or secondary modes. One problem with these 9 analyses was that the data plotted is a moving average based on 101 data points. With no breaks in data this equates to just over 8 years but as there are several gaps in the data this may distort matters. Averaging removes most of the short-term frequencies and makes it easier to perceive the general form.

Aberdeen .. Bergen .. Narvik

Reykjavik .. Murmansk .. Barentsburg

Lerwick .. Tiksi .. Torshavn
Figure 13
Each of the 9 Tidal Gauges will now be looked at showing the initial data from NOAA Web Site, processed data showing best fit quadratic curve, residuals (actual value minus value on best fit curve), spectral analysis plots and tables of results. The tables are basically values from the software’s original use, which was variable star analysis. The first column is Frequency
(1/Period) in cycles per year. Time is the Period at which this Frequency occurs in Years. Theta has been referenced in this paper as Amplitude.
At this stage no curve fitting was carried out as in most cases there are 2 or more peaks. The Amplitudes used on the Spectral Analysis (amp) and the Amplitudes of the Sinusoidal Curves (AMP) have been studied for known multi sinusoidal curves and it has been found that the Amplitudes for a pair of curves, 1 and 2, are related by the equation
AMP2 = AMP1 * SQRT(amp2/ amp1) (Equation 2)
Using this it can be estimated the relative dominance of each curve shown on the Spectral Analysis graphs.

Bergen

Narvik

Narvik (reduced data set)
The data before 1947 has been discarded due to the large gap in readings and the suspicious initial data values close to the beginning of the data.

Reykjavik

Murmansk

Barentsburg

Lerwick

Tiksi

Torshavn

Coming Soon:
Having applied spectral analysis to a number of Tidal Gauges, Part 2 will use the findings to derive sinusoidal curves.
Discover more from Watts Up With That?
Subscribe to get the latest posts sent to your email.