What is the Global Average SST? – Watts Up With That?

By Andy May

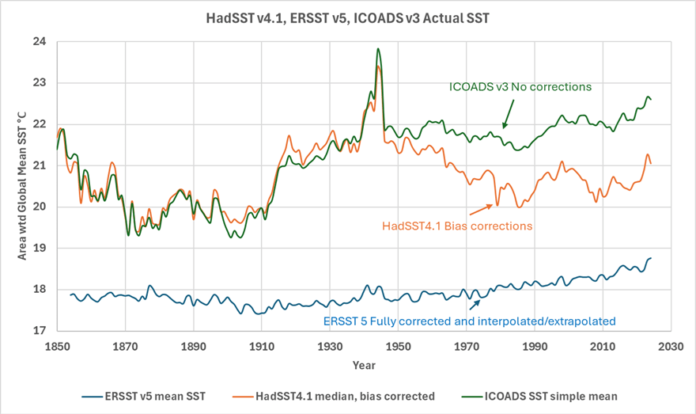
The global average SST (Sea Surface Temperature) is a very important component of the global average surface temperature for the simple reason that the global ocean covers almost 71% of Earth’s surface. So, we downloaded the gridded SST data from 1850 through 2024 from the Hadley Centre (HadSST v4.1), NOAA (ERSST v5), and NOAA’s SST data repository (ICOADS v3) and then plotted the data in figure 1.

There are good reasons for the large spread of SST values in figure 1 and we will go through some of them in this post, but the original question remains, “What is the global average SST?” The global average surface temperature has supposedly increased around one degree since 1850, but the differences in the records plotted are larger than that.

ICOADS (International Comprehensive Ocean-Atmospheric Data Set) is the ultimate source of nearly all the data plotted in figure 1. Nearly all the original ship, buoy, and other raw data used by the Hadley Centre and the NOAA ERSST (Extended Reconstructed SST) group comes from ICOADS v. 3. In addition to collecting the raw data they also provide a simple mean gridded product of their own as shown in figure 1 in green. All the global average temperature data plotted in this post is area weighted. The grids utilized by the agencies are latitude and longitude grids and while the latitudes are spaced the same everywhere, the longitudes are not, they are around 111 km apart at the equator and converge to zero at the poles so the area of each grid cell changes with the cosine of the latitude, which I corrected for. The ICOADS simple mean plotted in figure 1 is as close to the raw data as you can get.

The Hadley Centre provides a lot of information about the steps they take to reach their final global average SST and at several steps they provide an intermediate product (see here). This is very commendable and educational. We downloaded their final “core” temperature anomaly, the unadjusted anomaly, and the “actuals” dataset in degrees C. These are plotted in figure 2.

The process that the Hadley Centre uses to get from the ICOADS raw data plotted in figure 1 to the “core” HadSST product shown in figure 2 is described in several papers (Rayner, et al., 2006), (Kennedy J. J., Rayner, Smith, Parker, & Saunby, 2011), (Kennedy J. J., Rayner, Smith, Parker, & Saunby, 2011b), and (Kennedy J. , Rayner, Atkinson, & Killick, 2019).

Their process is made difficult because their measurement “stations” are constantly moving, except for a few tethered buoys. So, their first step is to construct a reference “climatology” grid. In the case of the Hadley Centre this is a global ocean one degree by one degree grid. Each usable ocean grid cell must have monthly average values for the reference period of 1961-1990. Most of these values are measured from ships. Not all grid cells had actual measurements in the reference period for some years or months and interpolation and some extrapolation in both time and space was required to complete the 1961-1990 climatology (Rayner, et al., 2006).

A special averaging function that trims extreme values, called a winsorized mean, is used to compute the values for each reference and monthly measurement cell (Rayner, et al., 2006). Later the one-degree grids are combined into the larger five-degree grids that are used to produce the averages shown in this post and the final “core” SST anomaly product plotted in figure 2 in orange.

The Hadley Centre starts with the ICOADS v. 3 raw data shown in figure 1, but they exclude some of the data either to use later as a quality control check, or because they consider it inferior data (Kennedy J., Rayner, Atkinson, & Killick, 2019). The usable data is first placed in its grid cell and converted into an anomaly by subtracting the climatology reference mean for the month from the monthly average value (Kennedy J., Rayner, Atkinson, & Killick, 2019). The measurement is obviously not from the same source as the climatology reference value.

After the initial anomalies are computed, the potential biases are computed for the individual values based on the data source. It might be a bucket sample taken over the side of a ship, in this case the type of bucket and bucket insulation, if any, is taken into account. It might be from a ship engine water intake, in that case the location of the thermometer relative to the engine is taken into account, and so on. Using the data they have about each measurement, a possible suite of “realizations” of the biases are generated and the median value of these hypothetical biases is selected to compute a “bias-corrected” anomaly. The resulting bias-corrected actual temperature values are averaged in figure 2 and shown as an “Actual” temperature in degrees C in light green in figure 2. The raw anomalies, without a bias correction, are shown in figure 2 as a dark blue line. It is interesting that the bias corrected actual temperature has a different shape than either the final core anomaly or the uncorrected anomaly. I’m not sure what to make of that.

Since most of the measurements used to compute SST are moving (ships and drifting buoys) and they all have different biases and measurement methods that change over time, building a coherent and consistent SST global average temperature record is a challenge.

The most heavily processed estimate of global ocean temperatures is the ERSST v. 5 reconstruction. We don’t have any intermediate data like we have for the HadSST reconstruction, but we have Boyin Huang, et al.’s description of the process (Huang, et al., 2017). Like the HadSST process, ERSST v. 5 starts with the ICOADS v. 3 dataset. The ERSST team then goes through a process that validates observations, discarding those that do not meet their quality control checks, bias corrects the data, cross checks with neighbors, and excludes outliers. They directly use ARGO data rather than using ARGO as a validation dataset like the HadSST team do. In ERSST, ARGO observations are weighted by 6.8 times the weight of ship observations.

The ERSST process utilizes the HadISST data to locate ice cover. When a grid cell is 90% covered with ice or more the SST in the grid cell is set to -1.8°C. Partial coverage is linearly interpolated between the reconstructed grid cell value and -1.8°C (Huang, et al., 2017). Since -1.8°C is the temperature where seawater freezes this makes some sense, but currents do exist under ice caps and clearly the sea surface temperature under the ice is not a uniform -1.8°C. Their assumption is a speculative oversimplification when we are trying to estimate surface warming rates on the order of 0.1°C/decade.

Their reconstruction process includes both interpolation and extrapolation. By making these assumptions, the ERSST reconstructed grid is more complete than the HadSST grid, as shown in figure 3.

ERSST provides a very full grid. HadSST is more conservative but still uses interpolation and some extrapolation to produce as full a grid as they can. Compare these two maps to the ICOADS map of the actual data in 2024 shown in figure 4.

The ICOADS simple mean temperature uses all values, whereas both HadSST and ERSST reject anomalous values, so the ICOADS coverage as mapped in figure 4, is as good as it gets, at least with respect to the actual measurements.

Comparing the maps in figures 3 and 4 shows us one of the reasons why the ICOADS global average temperature is the highest in figure 1 and the ERSST temperature is the lowest. The ERSST average includes a lot of assumed low values under polar ice that are unused null grid values in the ICOADS and HadSST averages. The differences between HadSST and ICOADS are due, at least in part, to the difference in the cell sizes. The ICOADS cells are 2×2 degrees and the HadSST cells are 5×5. These are areas of 49,000 sq km and 308,000 sq km respectively at the equator. The larger HadSST cell size allows for smaller areas without any measurements to be incorporated into larger cells that have values. In other words, the larger cells spread what data exists over larger areas.

So far, we’ve only looked at the distribution of measurements and final values for 2024. How does the amount of data vary over time? We have detailed data for both ICOADS and HadSST on observations and have plotted it in figure 5.

Figure 5 shows that HadSST reports a lot more observations per cell than ICOADS, even more than would be expected due to the larger HadSST cell size. Further, at latitude 30S, HadSST reports as many observations as at 30N for 2024, these observations are not seen in the ICOADS 2024 dataset. The ICOADS data is not interpolated or manipulated, thus the observations plotted in the lower half of figure 5 are real. HadSST does not interpolate, extrapolate, or infill cells to the extent that ERSST does, but they obviously do some. The methods used to interpolate, infill, and extrapolate values in HadSST are described in part in Rayner et al. (Rayner, et al., 2006). A lot of this is accomplished when combining the initial one-degree cells into the final five-degree cells.

It is apparent that we don’t know what the global average SST is at the accuracy required to detect a warming rate of 0.1°C/decade. The raw data (ICOADS) does not compare well to the processed results, as shown in figures 1 and 2.

The ICOADS simple mean is the closest to the actual measurements and is preferred for that reason. Comparing it (in green) and the HadSST 4.1 Actual bias-corrected values (light blue) in figure 6 to the more highly processed standard anomalies shows that all estimates, anomaly or otherwise, are suspect before 1990 and even afterward.

In figure 6 the ERSST, ICOADS and HadSST 4.1 actual temperatures are converted to anomalies by subtracting their respective 1961-1990 means from each grid cell value. This is different from the normal procedure of computing each anomaly by subtracting its individual reference mean from each value before processing and populating the grid. The normal procedure was used to build the plotted final median core HadSST 4.1 anomaly in figure 6. However, even though the other anomalies were computed differently, the ICOADS anomaly is a fairly close fit to the ERSST and final HadSST anomalies from the early 1990s to 2024.

The HadSST bias-corrected Actual values, converted to an anomaly, do not match most of the other anomalies very well, even after 1990, which is a bit confusing. The data quality over World War II (WWII) is very poor as discussed by Huang, et al. Kennedy, et al. (2019) also discuss the data quality over this period, especially the sharp drop at the end of war, and say it is due to a large change in the areas sampled by the global fleet. Some of the sudden post-war drop may also be due to a change in the ship sampling methods. This anomaly is hidden in most datasets because the anomalies in most datasets are computed before processing begins masking the measured jump and fall in actual SST. Sometimes when viewing Earth through a microscope you can miss the mountains. The original papers do not include plots of actual temperature, but the WWII data problem can be seen in Kennedy, et al.’s (2019) bias plots in their figures 6, 7, 8, 9, 10, and 13.

The agreement between the estimated anomalies is also poor prior to 1912, which is largely due to poor sampling, the ICOADS observations prior to 1912 generally never exceed 5,000 and peak between 30N and 45N at only 9,000 observations. While good reasons exist for all the problems identified in this post and for all the corrections applied by the HadSST and ERSST teams, this does not mean they are getting the right answer.

Thus, the global average SST, the most important component of global average surface temperature, is largely unknown before the early 1990s and even after 1990 there is some doubt. The doubts about the SST average and the doubts about the land record combined with the very small amount of warming since the beginning of the 20^th century (about one degree) cast considerable doubt, at least in my mind, about estimates of modern global warming. I don’t doubt that the world is warmer, on average, since 1900, but I don’t think we know how much warming has occurred with any accuracy. I also don’t think we necessarily have the trend or trends right, is part of the WWII “hump” real? I don’t think we know.

Huang, B., Thorne, P. W., Banzon, V. F., Boyer, T., Chepurin, G., Lawrimore, J. H., . . . Zhang, H.-M. (2017). Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. Journal of Climate, 30(20). doi:10.1175/JCLI-D-16-0836.1

Kennedy, J. J., Rayner, N. A., Smith, R. O., Parker, D. E., & Saunby, M. (2011). Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850; 1. Measurement and sampling uncertainties. Journal of Geophysical Research, 116. Retrieved from https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2010JD015218

Kennedy, J. J., Rayner, N. A., Smith, R. O., Parker, D. E., & Saunby, M. (2011b). Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850: 2. Biases and homogenization. J. Geophys. Res., 116. doi:10.1029/2010JD015220

Kennedy, J., Rayner, N. A., Atkinson, C. P., & Killick, R. E. (2019). An ensemble data set of sea-surface temperature change from 1850: the Met Office Hadley Centre HadSST.4.0.0.0 data set. JGR Atmospheres, 124(14). Retrieved from https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2018JD029867

Rayner, N. A., Brohan, P., Parker, D. E., Folland, C. K., Kennedy, J. J., Vanicek, M., . . . Tett, S. F. (2006). Improved Analyses of Changes and Uncertainties in Sea Surface Temperature Measured In Situ since the Mid-Nineteenth Century: The HadSST2 Dataset. J. Climate, 19, 446-469. doi:10.1175/JCLI3637.1